Operación Producto Cartesiano
Tipo: Binaria
Sintaxis:
Tabla1 X Tabla2
Descripción: Concatena cada una de las tuplas de Tabla1 con cada una de las tuplas de Tabla2, una a una. Para entender mejor esta operación, suponga la siguiente situación expresada:
Tabla1: Tiene 10 tuplas y 8 atributos.
Tabla2: Tiene 7 tuplas y 9 atributos.
Entonces,
Tabla1 X Tabla2 tiene 70 tuplas y cada tupla tendrá 17 atributos.
Ejemplo: Suponga las siguientes dos tablas:
| Avión |
|
Matrícula PK Marca No.horasvuelo Codigo-aerolinea |
|
FK: Codigo-aerolinea referencia a Aerolinea(codigo) |
| Aerolinea |
|
Codigo Nombre AñoFundacion |
Y los datos de ambas tablas son los siguientes:
Tabla Avión
| Matrícula | Marca | No.horasvuelo | Codigo-aerolinea |
|
HK7800 |
Boeing |
520 |
10 |
|
HK8000 |
Airbus |
410 |
10 |
|
HK2300 |
Concorde |
215 |
20 |
|
HK7400 |
Boeing |
500 |
30 |
Tabla Aerolínea
| Código | Nombre | AñoFundación |
|
10 |
Avianca |
1950 |
|
20 |
Copa |
1966 |
|
30 |
Satena |
1945 |
Entonces el resultado de Avión X Aerolínea es el siguiente:
| Matrícula | Marca | No.horasvuelo | Codigo-aerolinea | Código | Nombre | AñoFundación |
|
HK7800 |
Boeing |
520 |
10 |
10 |
Avianca |
1950 |
|
HK7800 |
Boeing |
520 |
10 |
20 |
Copa |
1966 |
|
HK7800 |
Boeing |
520 |
10 |
30 |
Satena |
1945 |
|
HK8000 |
Airbus |
410 |
10 |
10 |
Avianca |
1950 |
|
HK8000 |
Airbus |
410 |
10 |
20 |
Copa |
1966 |
|
HK8000 |
Airbus |
410 |
10 |
30 |
Satena |
1945 |
|
HK2300 |
Concorde |
215 |
20 |
10 |
Avianca |
1950 |
|
HK2300 |
Concorde |
215 |
20 |
20 |
Copa |
1966 |
|
HK2300 |
Concorde |
215 |
20 |
30 |
Satena |
1945 |
|
HK7400 |
Boeing |
500 |
30 |
10 |
Avianca |
1950 |
|
HK7400 |
Boeing |
500 |
30 |
20 |
Copa |
1966 |
|
HK7400 |
Boeing |
500 |
30 |
30 |
Satena |
1945 |
A cualquier par de tablas se les puede hacer un producto cartesiano. Lo que sucede es que hay ocasiones en las cuales el resultado no tiene sentido.
Ejemplo: Listar la matrícula y marca de cada avión junto con el nombre de la aerolínea a la cual pertenecen.
Para solucionar esto en SQL, se sabe que se ejecuta la siguiente instrucción:
SELECT av.matricula, av.marca, ae.nombre
FROM Avion av INNER JOIN Aerolínea ae
ON av.codigo-aerolinea = ae.codigo
Si se analiza el producto cartesiano entre Avión y Aerolínea, el resultado son 12 tuplas, de las cuales 8 son tuplas espurias y 4 son tuplas verdaderas. Cuáles son las 8 tuplas espurias y cuáles son las 4 verdaderas?
Entonces, para hacer la anterior consulta en álgebra relacional, la operación es la siguiente:
Π matricula, marca, nombre (Ϭ código-aerolinea = codigo(Avión X Aerolínea))
Primero se hace el producto cartesiano, el cual da como resultado 12 tuplas. Luego se hace la selección, la cual selecciona las 4 tuplas reales y de estas 4 tuplas se proyectan los atributos a imprimir.
Como conclusión a este ejemplo, se puede afirmar que todo INNER JOIN es hecho a través de un producto cartesiano.
Ejemplo: Listar el número de horas de vuelo del avión que MÁS horas de vuelo tiene.
Hacer esto en SQL es muy sencillo:
SELECT max(No.horasvuelo)
FROM Avión
La explicación siguiente muestra cómo se llevaría a cabo esta instrucción en álgebra relacional.
Para uno saber cuál es el máximo número de horas de vuelo, se deben comparar TODOS los números de horas de vuelo. Eso está disponible en la tabla AVION, pero cada No.horasvuelo está en una tupla distinta, lo cual se constituye en un problema ya que no se tiene una operación que compare valores de un mismo campo en tuplas distintas.
El problema se solucionaría si tuviéramos el par de valores a comparar del atributo No.horasvuelo en la misma tupla. Como se logra esto?
Si se hace un producto cartesiano entre la tabla Avión consigo misma, cada tupla tendría dos No.horasvuelo y se tendría todas las parejas que habría que comparar. El producto cartesiano mencionado se muestra a continuación.
Avion X Avion
| Matricula | Marca | No.horasvuelo | Codigo-aerolinea | Matricula | Marca | No.horasvuelo | Codigo-aerolinea |
|
HK7800 |
Boeing |
520 |
10 |
HK7800 |
Boeing |
520 |
10 |
|
HK7800 |
Boeing |
520 |
10 |
HK8000 |
Airbus |
410 |
10 |
|
HK7800 |
Boeing |
520 |
10 |
HK2300 |
Concorde |
215 |
20 |
|
HK7800 |
Boeing |
520 |
10 |
HK7400 |
Boeing |
500 |
30 |
|
HK8000 |
Airbus |
410 |
10 |
HK7800 |
Boeing |
520 |
10 |
|
HK8000 |
Airbus |
410 |
10 |
HK8000 |
Airbus |
410 |
10 |
|
HK8000 |
Airbus |
410 |
10 |
HK2300 |
Concorde |
215 |
20 |
|
HK8000 |
Airbus |
410 |
10 |
HK7400 |
Boeing |
500 |
30 |
|
HK2300 |
Concorde |
215 |
20 |
HK7800 |
Boeing |
520 |
10 |
|
HK2300 |
Concorde |
215 |
20 |
HK8000 |
Airbus |
410 |
10 |
|
HK2300 |
Concorde |
215 |
20 |
HK2300 |
Concorde |
215 |
20 |
|
HK2300 |
Concorde |
215 |
20 |
HK7400 |
Boeing |
500 |
30 |
|
HK7400 |
Boeing |
500 |
30 |
HK7800 |
Boeing |
520 |
10 |
|
HK7400 |
Boeing |
500 |
30 |
HK8000 |
Airbus |
410 |
10 |
|
HK7400 |
Boeing |
500 |
30 |
HK2300 |
Concorde |
215 |
20 |
|
HK7400 |
Boeing |
500 |
30 |
HK7400 |
Boeing |
500 |
30 |
Lo que sigue es empezar a comparar cada par de valores del campo No.horasvuelo que hay en cada tupla. Pero surge un nuevo problema: en Avión X Avión, en cada tupla hay dos atributos llamados No.horasvuelo, por lo tanto, si necesitamos comparar ese par de valores hay que diferenciar, de alguna manera, los nombres de los atributos.
Es ahí donde entra a funcionar la operación de renombramiento. Si al hacer la operación de Avión X Avión, se renombra alguna de las dos “tablas” (Avión de la izquierda del producto o Avión de la derecha del producto), ya habría alguna manera de identificar los dos atributos No.horasvuelo.
Por lo tanto, con la explicación dada hasta el momento, tenemos la siguiente expresión del álgebra:
Avión X ρ Av (Avión)
lo cual da como resultado la tabla anterior.
El mecanismo para lograr la consulta requerida es la siguiente:
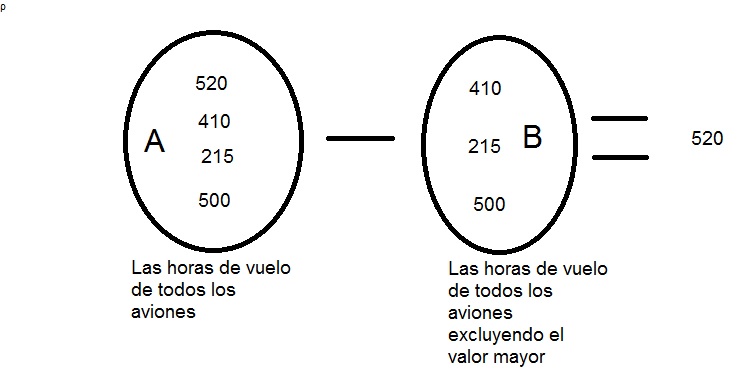
Fuente Propia.
Entonces,
A = Π No.horasvuelo (Avión)
C = Ϭ Avion.No.horasvuelo < Av.No.horasvuelo (Avión X ρ Av (Avión))
B = Π Avion.No.horasvuelo (C)
Las tuplas seleccionadas en C se muestran resaltadas en amarillo.
Avion X Avion
| Matricula | Marca | No.horasvuelo | Codigo-aerolinea | Matricula | Marca | No.horasvuelo | Codigo-aerolinea |
|
HK7800 |
Boeing |
520 |
10 |
HK7800 |
Boeing |
520 |
10 |
|
HK7800 |
Boeing |
520 |
10 |
HK8000 |
Airbus |
410 |
10 |
|
HK7800 |
Boeing |
520 |
10 |
HK2300 |
Concorde |
215 |
20 |
|
HK7800 |
Boeing |
520 |
10 |
HK7400 |
Boeing |
500 |
30 |
|
HK8000 |
Airbus |
410 |
10 |
HK7800 |
Boeing |
520 |
10 |
|
HK8000 |
Airbus |
410 |
10 |
HK8000 |
Airbus |
410 |
10 |
|
HK8000 |
Airbus |
410 |
10 |
HK2300 |
Concorde |
215 |
20 |
|
HK8000 |
Airbus |
410 |
10 |
HK7400 |
Boeing |
500 |
30 |
|
HK2300 |
Concorde |
215 |
20 |
HK7800 |
Boeing |
520 |
10 |
|
HK2300 |
Concorde |
215 |
20 |
HK8000 |
Airbus |
410 |
10 |
|
HK2300 |
Concorde |
215 |
20 |
HK2300 |
Concorde |
215 |
20 |
|
HK2300 |
Concorde |
215 |
20 |
HK7400 |
Boeing |
500 |
30 |
|
HK7400 |
Boeing |
500 |
30 |
HK7800 |
Boeing |
520 |
10 |
|
HK7400 |
Boeing |
500 |
30 |
HK8000 |
Airbus |
410 |
10 |
|
HK7400 |
Boeing |
500 |
30 |
HK2300 |
Concorde |
215 |
20 |
|
HK7400 |
Boeing |
500 |
30 |
HK7400 |
Boeing |
500 |
30 |
Y al hacer B, es decir, al proyectar los valores de No.horasvuelo de la izquierda de dichas tuplas, obtenemos B.
Por lo tanto, la solución a la consulta es A – B.
Qué pasa si lo que se necesita es listar el número de horas de vuelo del avión que MENOS horas de vuelo tiene?